量子力学のおすすめ。入門レベルから院試対策の参考書はこれ！

量子力学は最先端研究へ進む登竜門

宇宙の初期や力の伝播、物質の究極の要素といった分野では、ミクロの世界を扱います。

ミクロの世界は不思議なもので、私たちが考えている常識が時には通用しないこともあります。

 

 

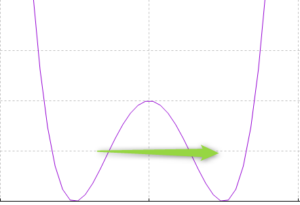
例えば、上のグラフのようなある断熱ポテンシャルを考えます。

古典力学の世界、すなわち日常で体験している世界では、左側から右側に行くためには、山を飛び越えるだけのエネルギーを与える必要があります。

山を乗り越えるだけのエネルギーがなければ、右側の谷には行けないからです。

 

ところが量子力学の世界では、まれに山より低いエネルギーしか与えられなくても、左側から右側にすり抜ける現象が発生します。

これをトンネル効果と呼びます。

トンネル効果は、物理的な研究のみならず、工学的な応用にも利用されています。

 

このように量子力学は、時には私たちの常識が通用しないこともあるのです。

しかし、この量子力学特有の世界は、物質の究極の構造：クォークを調べる際や力の伝播を伝える粒子などを調べる時に必ずでてきます。

近年はこの分野の研究も進み、粒子の構造のみならず、ブラックホールや宇宙初期にどのようにして物質ができたのかにも関わりを持っているのです。

 

量子力学の世界は私たちの常識が必ずしも通用しないので、このギャップを理解できるかどうかが鍵になるだけでなく、量子力学を記述するシュレディンガー方程式には「演算子」と呼ばれるものが出てきます。

便利な道具なのですが、演算子が普通の文字のように扱っていたりするので、演算子と普通の文字が同等であるという部分のギャップに苦しんだりすることもあるかもしれません。

そのため、量子力学は最先端研究の登竜門とも言われています。

 

量子力学の書籍はたくさん出ていますが、ここでは初めて量子力学を学習する人でも学習できるよう、段階を追って参考書を紹介いたします。

量子力学を学習するに当たっての前提

量子力学は、比較的新しく誕生した学問です。

そのため、いきなり量子力学の学習を始めてもいくつか学習していることが前提にしている参考書がほとんどです。

まずは前提を学習することが量子力学を理解する上では大切になります。

 

量子力学は力学や電磁気学を研究していくうちに、これらの学問で説明されてきた内容では説明がつかない現象が発生したことから始まっています。

そのため、物理学の範囲では

 

• 力学
• 解析力学
• 電磁気学
• 熱力学
• 統計力学
• 波動

 

といった内容を学習していることが前提になっています。

当然のことながら、これらの分野に必要な数学

 

• 解析学
• 線形代数
• ベクトル解析
• フーリエ解析
• 常微分方程式
• 偏微分方程式

 

といったところも、最低限講義で学習する内容は自分で計算を進める上では必須です。

おすすめの参考書

ミクロの世界を理解するための前提を復習したい

量子力学はミクロの世界を扱ったものです。

元素が物質の究極の構造だと考えられていた時代もありましたが、研究が進むにつれ、原子核と電子によって構成されていることがわかりました。

さらに、原子核は陽子と中性子、陽子と中性子はクォークでできていることも研究から明らかになってきています。

時代が進むにつれ、ミクロの世界が広がっていきました。

この流れの中で、量子力学が誕生し、発展していったのです。

量子力学はミクロの世界を支配する基本法則であるということを理解するためにどのようにして量子力学が誕生したのかを知っていると、理解しやすいかと思います。

 

この本は、従来原子物理学と言われていた部分を扱った内容を記載したものです。

IとIIの二冊がありますが、Iは原子の世界から量子力学が誕生するまでの流れの要点を記載したものになっています。

Iには量子力学の誕生までが書かれているため、本格的な量子力学の内容については触れていません。

しかし、今までに学習した内容も量子力学のテキストに出てきますので、今まで学習した内容のうち、最低限何を学習したらよいかというものの指針となる参考書です。

 

量子力学の入門書

ここでは、量子力学の入門書を3種類紹介します。

量子力学のテキストとして用いられているところもあるくらい有名なテキストです。

学部レベルの力学・電磁気学とそれに付随する数学を学習していれば、読むことができるよう配慮されています。

量子論から量子力学までの基本部分を一通り学習したいときには、上記の量子力学2冊で量子力学全般が見えてきます。

また、数学的に省略しているところがなく、計算過程が記載されているので、式の導出についてフォローしやすい入門書ですが、本格的な量子力学の部分に突入する「井戸型ポテンシャル」といった部分も深く掘り下げられている点も評価できます。

ただ、誤植も若干あるので、 読み始める前に裳華房の該当図書のページで正誤表をダウンロードしておくとよいでしょう。

目次（量子力学I（1-8）、量子力学II（9-13））

1. 光の波動性と粒子性
2. 原子核と電子
3. 過渡期の原子構造論
4. 波動力学のはじまり
5. 波動関数の物理的意味
6. 量子力学の成立
7. 井戸型ポテンシャル
8. 調和振動子
9. 角運動量
10. 原子の構造
11. 近似法
12. 散乱問題
13. 輻射と物質の相互作用

「量子力学の冒険」は、フーリエの冒険の続編という位置づけになっています。

そのため、「量子力学の冒険」はフーリエ展開を学習していることが前提になります。

内容は、量子力学の誕生を時系列に追いながら、シュレーディンガー方程式の導出までになります。

シュレーディンガー方程式を使ってわかることなどは、別の書籍で学習します。

 

わかりやすいよう絵を入れたり説明を入れたりしていますが、フーリエの冒険とは違い、数式がたくさん出てきます。

でも、進み方はゆっくりですので、数式を恐れずに一つ一つ紙と鉛筆を使いながら解いていってください。

目次

1. Max Planck and Albert Einstein 光は何者だ!?
2. Niels Bohr 前期量子論
3. Werner Heisenberg 量子力学の誕生
4. Luis Victor de Broglie and Erwin Schr¨odinger 新しい描像
5. Erwin Schr¨odinger さらば、マトリックス
6. Max Born and Werner Heisenberg 新世界への出発

「量子力学のを学ぶに当たっての前提」に書いた内容を理解していることが前提ですが、量子力学の基本となる項目について解説をしています。

内容は後述する量子力学IとIIの抜粋した上で、より易しい解説となっています。

特にシュレーディンガー方程式は詳しく解説されています。

 

本書シリーズの特徴として、各章にもうけられた例題が豊富であり、演習問題もついているので、量子力学の理解の助けになります。

物理学は数学との結びつきが強いですので、例題や演習問題を自分の手で計算して解くという作業が大切になります。

そういった点で、例題や演習問題が豊富で、丁寧な解説があるのは助かります。

 

・目次

第1章　量子力学へのあゆみ
第2章　光と電子の波動性と粒子性
第3章　シュレーディンガー方程式
第4章　1次元の問題-束縛状態
第5章　1次元の問題-反射と透過
第6章　中心力場のシュレーディンガー方程式-3次元の場合
第7章　量子力学の一般的性質
第8章　角運動量とスピン
第9章　電磁場中の荷電粒子
第10章　同種粒子
第11章　近似法

 

一通りの内容を演習問題と併せて学習したいときの参考書

この二冊の本が出版された後、もう少し基本的な内容のものも出してほしいという要望があり、前述の基礎量子力学が出された経緯があります。

前提条件で書いた数学や物理の内容を学習していることが前提の他、群論やリー代数もある程度学習しているとより理解が深まります。

数学的な部分の解説もありますが、やや厳密性に欠けるので、このあたりをつめたい場合には、該当箇所についての数学のテキストで学習するとよいでしょう。

とはいえ、豊富な例題と演習問題、そして具体的な計算ができるようになっているので、この二冊で量子力学の一通りの内容を理解し、計算できるだけの力がつくでしょう。

院試レベルであれば、基礎量子力学、量子力学I、IIの三冊で十分です。

レベルとしては原子核、素粒子物理といった量子力学を使って研究をする文には十分ですが、量子力学そのものを深く追求する人は、さらに別のテキストで学習したほうがいいかもしれません。

また、テキストが出版された後、素粒子物理の世界で次々と新たな発見がなされています。

最先端の内容や言及については、執筆した当時の内容であるということに留意してください。

相対論的量子力学の参考書

量子力学もある条件下では相対論を考慮する必要がでてきます。

本来であるならば、場の量子論で論ずる必要がでてきますが、場の量子論を学習する前に相対論的量子力学の内容を学習しておく必要があるかもしれません。

この「相対論的量子力学」は、場の量子論を意識的に避けて、議論をしています。

理論式を導き出すことに重点が置かれていますので、どのように理論式がでてきたかをしるための、数少ない和書です。

目次

1. Ｄｉｒａｃ方程式
2. 電磁場の量子論
3. 電磁場の量子論の応用
4. 散乱の一般論
5. 付録．時間反転

 

なお本格的に学習したいときは洋書「Relativistic Quantum Theory」で学習します。