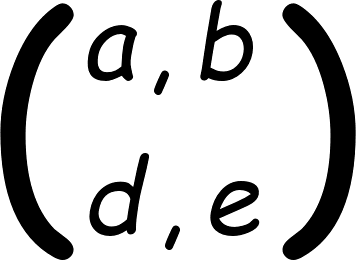量子力学や化学(特に量子化学)で群論がでてきます。
より深く学ぶ際には、群論は必要な知識です。
しかし、群論は奥が深いので、説明の前提として、群の表現に必要な数学の知識を持っていることが前提で書かれているテキストが多くあります。
テキストで群論を学ぼうとするにはあまりにも前提が多すぎるのです。
けれども、量子力学を必要としている君にとって、まずは概略でだけでも群論を理解していると、その後の量子力学の学習の助けになります。
ここでは、群論の入門書を紹介いたします。
群論を知らなくても大丈夫?!
物理や化学には、対称性に関する問題がでてきます。
物理では量子力学・相対論だけでなく、力学でも使う場合があります。
対称性の意味をうまく利用することで、群論を知らなくてもこれらのことの本質的な部分は理解できてしまうことがあります。
しかし、より専門的なテキストや論文には記号や用語が出てきます。
つまり、本質的な部分の理解だけであれば、群論は使わなくてもなんとかなります。
ですが、より深く学ぼうとするときに、群論で使われる言葉や意味を知らないと、 テキストや論文を読みこなすことができないという問題が発生します。
さきほど、「群論を知らなくても、対称性の意味をうまく利用することで、本質的な部分は理解できてしまう。」と書きました。
このことは、群論の本質的な部分を難しく考えなくても理解できてしまうと言ってもいいかもしれません。
ただ、用語が難しいのです。
だから、群論はあまり身構える必要はないのですよ。
おすすめの参考書
対称性から群論へのやさしいアプローチ
数学科以外の専攻の君が、群について学習する時に読む参考書は、数学科で数学の基本を学習していることが前提で書かれているテキストが非常に多くあります。
しかし、数学科で学習するような内容を学習していない、物理や化学などの専攻している君にとっては、いきなり出てくる数学記号でつまづきやすいという弱点がありました。
「化学や物理のためのやさしい群論入門」では、物理や化学を専攻している君を対象に、できる限りやさしく群を学習できるよう解説されています。
応用例としては、分子や結晶など化学分野の内容が多いのですが、物理専攻の君でも群の基本を理解するのには、ちょうどいい内容となっています。
目次
- 分子の対称性と対称操作
- 群
- 点群
- 行列式と行列
- ベクトルとその変数
- 群を行列で表現する
- 群の表現論 – 指標表
- 群論の量子力学
- 分子の振動状態
- 分子の電子状態
- 遷移金属錯体(本文未収録。サポートサイトでダウンロード可能)
- 結晶の対称性と空間群(本文未収録。サポートサイトでダウンロード可能)
誤字訂正や続きのコンテンツは、以下のサイトでダウンロードすることができます。
群論を学習するに当たって必要な数学の知識について、かなりのページを割いて解説しています。
線形代数などで学習している内容も含まれているので、その部分はさっと見る程度で済む章もあるかもしれません。
しかし、それは講義の進捗(しんちょく)具合でも変わることです。
こういう内容を知っておくと群論が理解できるという点でも、前提知識をあまり必要とせず、解説している点がおすすめです。
群論を使った物質の対称性を学習するのに適した参考書
量子力学や固体物理、化学分野では、対称性に関する内容がよく出てきます。
「物質と対称性と群論」は、群論が物理や化学でどのように応用されているかについて、解説している書籍です。
目次
- ブラベー格子と結晶系
- 点群
- 空間群
- 群論入門
- 量子力学の復習
- 球対称場における原子の状態
- 配位子場理論
- 分子軌道法
- 分子振動
- バンド理論
- テンソル
目次に書いてあるとおり、かなりの内容を群論の応用に当てています。
そのため、群論そのものは「化学や物理のための やさしい群論入門」など別の参考書で学習する必要があります。
「物質と対称性と群論」も化学よりの応用例が多いのですが、固体物理と接点はあるので、近い分野を学習している君に取っては、非常に参考になるテキストです。
行列から群への橋渡しをする参考書
群論には、行列が使われています。
論理を追えば、抽象的な記述になってしまいますが、群の実例を交えながら解説することで、群についてのイメージがつかめることでしょう。
「キーポイント 行列と変換群」は行列から群論への橋渡しをしている参考書です。
目次
- ベクトルを回転してみよう
- 行列は回転を引き起こす
- 役に立つ行列の基礎操作
- ベクトル空間と変換群
- 行列の指数関数
- 行列の指数関数の微分と行列式
- 3次元の回転
- ユニタリ行列と3次元の回転
- ベクトル、テンソル、そしてスピノール
- 最後のリー代数の話
予備知識としては、微分・積分と線形代数(ベクトル・行列)の知識が必要ですが、解説も具体的な話を出しているのでワカリヤス内容となっています。
ただ、ポイントに絞って解説してあるので、少し物足りなく感じるかもしれません。
あくまで群論への橋渡しを担う参考書になっています。
けれども、いきなり群論はハードルが高いなと思っている君には、「キーポイント行列と変換群」は、群を学ぶ前に助走をつけるにはもってこいの参考書です。