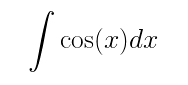微分方程式は数学分野に限らず、物理分野でも頻出します。
出てきたときに学ぶという方法もありますが、その場合でも基本的な微分方程式の計算はできていると、出てきた単元の学習スピードがあがります。
ここでは、物理などの単元の演習で計算ができるようになるための微分方程式の問題集を紹介します。
演習量は多いほどいい?
何も見なくてもサッと解けるようになるまでには、ある程度の演習量が必要です。
ただ、演習が必要だからと言って、量をこなせばいいかというと、そうでもありません。
もちろん、数をこなせばサッと解けるようになることでしょう。
しかし、大学では他の講義の予習・復習があります。
そのため、一つの講義の予習・復習に時間を大幅に割くことは難しいのです。
バランスを保つためにも、適切な演習量の問題集を選ぶ必要があります。
おすすめの問題集
常微分方程式メインに学習する時の問題集
問題は、証明問題も収録されていますが、どちらかというと方程式を解く問題が多いです。
講義で学習した内容から応用問題まで収録されています。
基本的な問題が出題される大学院の院試問題であれば、「演習微分方程式(新版)」で対策できます。
解説も詳しく載っていますので、演習の1冊としては十分でしょう。
ただし、偏微分方程式の章は少なめですので、後述する演習書を活用してもいいかもしれません。
後述の「微分方程式演習 (数学演習ライブラリ」と同じ出版社で色も似ていますので、購入する際には注意してください。
目次
- 微分方程式の基礎
- 1階常微分方程式
- 高階微分方程式
- 高階線形微分方程式
- 整数級に関する解法
- 全微分方程式と連立微分方程式
- 偏微分方程式
- フーリエ解析とその応用
偏微分方程式メインで学習したいときの参考書
前述の「演習微分方程式(新版)」と同じ出版社から出版されています。
色も似ていますので、購入する際には注意してください。
「微分方程式演習 (数学演習ライブラリ)新訂版」は、前述の「演習微分方程式(新版)」よりも若干難しめの問題まで収録されています。
また、偏微分方程式の問題が多くなっている分、常微分方程式の演習量が少なくなっています。
易しめの問題はテキストにある演習問題でこなし、少し難しめの問題までを演習するときに、「微分方程式演習 (数学演習ライブラリ)新訂版」を活用します。
さらに、問題演習には定理の証明なども「演習微分方程式(新版)」よりも多めになっています。
「演習微分方程式(新版)」は常微分方程式のウエイトが高い問題集でしたが、「微分方程式演習 (数学演習ライブラリ)新訂版」は常微分方程式、偏微分方程式ともに複数の章をもうけてあります。
このように常微分方程式・偏微分方程式の問題を両方こなしたい場合には、「微分方程式演習 (数学演習ライブラリ)新訂版」がおすすめです。
目次
- 第1章 1階常微分方程式
- 第2章 2階常微分方程式
- 第3章 近似解と存在定理
- 第4章 高階微分方程式と連立微分方程式
- 第5章 フーリエ解析
- 第6章 巾級数解
- 第7章 偏微分方程式序論
- 第8章 楕円型偏微分方程式
- 第9章 双曲型偏微分方程式
- 第10章 放物型偏微分方程式
計算過程がわからないときに使う問題集
マセマシリーズの特徴は、計算過程が事細かに掲載されていることです。
通常の問題集や参考書では、学習の前提条件にしている内容の部分は、省かれているからです。
この省かれている部分でつまづいてしまうと、手がかりがないので、そこから先に行くのは大変になってしまいます。
そのようなときに活用するのがマセマ シリーズなのです。
演習でつまづいて先に進めなくなってしまったときに、マセマシリーズの問題集を使って演習して、計算力をつけるといいでしょう。